이번 글에서는 회귀의 첫 시작이자 개념에 대한 정리 글이다. 깊게 다루지는 않겠다.
1. 회귀 (Regression)
1.1 회귀?
- Y=f(X)에 대하여 입력 변수(X)와 출력 변수(Y) 간의 관계를 모델링하는 지도학습의 대표적인 유형
- 여기에, 오차 e를 추가하는데, 실제 데이터에 존재할 수 있는 잡음 혹은 유실 발생에 대응하고자
- 입력 변수 X에 대해 연속형 출력변수 Y를 예측 (분류에서는 y의 변수: 이산형)
- 한 변수의 원인이 어떤 변수들인지 분석하는 방법 (즉, 독립변수 Xi와 종속변수 Y)
1.2 회귀의 종류
- 독립변수의 수에 따라 단순회귀분석, 다중회귀분석
- 독립변수의 척도에 따라 일반회귀분석, 더미변수를 이용한 회귀분석
- 독립변수와 종속변수의 관계에 따라 선형회귀분석(직선), 비선형 회귀분석(직선x)
y = β0 + β1x + β2x^2 + β3x^3 -> β0 + β1x1 + β2x2 + β3x3* 회귀모델의 선형성은 X가 아닌 회귀 계수들(베타)을 기준으로 생각하는 것 (즉, X의 제곱수들 때문에 비선형인게 아님!)
2. Simple Linear Regression
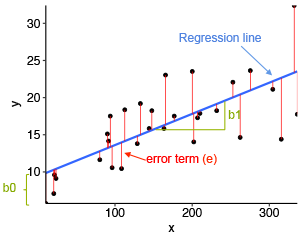
- 이 점들을 동시에 지나는 직선은 없지만, 두 변수(x,y)의 관계를 가장 잘 나타낼 수 있는 직선을 구하는 것!
- 최소제곱법 : 잔차(추정값-관측값)의 제곱합 값이 최소인 직선을 찾는 방법.(그림에서는 빨간선이 잔차값)
<장점>
- 상관관계를 정확하고, 수학적으로 설명할 수 있음
- 예측할 수 있음 (도출한 관계식에 새로운 값을 대입하여)
3. 회귀 모델의 기본 가정
회귀모델은 '데이터와의 오차합이 가장 작은 선'을 찾는 작업? 50%는 맞았다!
실제 회귀 모델링을 할 때는 잔차가 최소가 되는 선을 찾기 전에 전제 조건이 선행되어야하는데,
<조건> 데이터의 실측치와 모델의 추정치 사이의 잔차가 i.i.d (Independent and Identically Distributed random) 성질 만족
-> 잔차가 단순히 현실 세계에 존재하는 잡음 or 고려하지 못한 속성 때문인지 알고자 i.i.d 확인할 필요가 있다!
-> 잔차의 기대치(평균)가 0이고, 평균으로 회귀하는지?
- 잔차의 분포는 정규 분포여야하는 '잔차의 정규성' -> 가우스의 정규분포
- 잔차와 독립변수 X 사이에 상관관계가 없고, 자기 자신과도 상관이 없어야하는 '잔차의 독립성'
-> 잔차와 X의 scatter plot, auto regression류 모델 - 잔차의 분산이 항상 일정한 '잔차의 등분산성' -> 잔차와 X의 scatter plot
위 조건을 모두 만족한다면? 잔차는 평균으로 회귀!!!!
3.1) 회귀분석의 기본 가정(1) - 잔차의 정규성
- 오차의 확률분포가 정규분포를 따르는 것이 정확한 모델.
(정규 분포 자체가 원래 오차에 대한 확률 분포이기 때문)
오차의 성질을 연구하던 중 '가우스의 정규분포' 발견!
기술이 발달하지 못해, 눈으로 관측하면서 발생하는 오차의 차이값들을 분석해보니,
이 값들이 평균에 근접할 수록 발생확률이 높고 평균에서 멀어질수록 확률이 떨어지는 분포 규칙을 따른다.
즉, 어떤 모델이 데이터의 성질을 잘 설명한다면,
-> 잔차는 잡음만 남게 되고, 이런 잡음의 분포가 정규분포!
만약, 잔차의 분포가 정규분포가 아니라면?
-> 잔차는 단순한 잡음 뿐 아니라, 내가 반영하지 못한 어떤 특징이 포함되어있구나를 의미한다. (i.i.d로 확인!)
3.2) 회귀분석의 기본 가정(2) - 잔차의 독립성
잔차가 독립이 아니라는 것은? 잔차가 어떤 패턴을 가지고 있다는 것이다.
만약 모델을 정확히 만들었다면, 잔차는 단순 잡음인 것이니까 아무런 특징도 없어야한다!
이를 위해서는 두 가지 관계를 확인하면 된다.
1) X와의 상관성을 확인하는 가장 쉬운 방법 : 피어슨 상관 계수 구하기
2) 자기 자신과의 상관성을 가질 경우 : auto regresion 류 모델 (잔차의 자기 상관성을 반영한 모델)
잔차가 독립성을 가지면, 데이터의 특성에 영향을 받지 않고 원래의 확률인 정규 분포를 그대로 따른다.
-> 예측치가 데이터의 값에 영향을 받아 실측치에서 크게 벗어날 확률!이 매우 낮음.
3.3) 회귀분석의 기본 가정(3) - 잔차의 등분산성
마지막으로, 분산이 항상 일정한지 여부!를 확인해야한다.
잔차와 x 사이의 관계를 scatter plot으로 그려보면, 잔차의 퍼짐 정도가 일정한지, 점점 커지는지 확인이 가능하다.
잔차의 분산이 일정하지 않으면, (특히 발산 형태) 정규 분포를 잘 띄고 있더라도, x값이 커질 수록 점점 평균에서 크게 벗어난 값을 가질 확률이 커진다. 그러면 평균으로 회귀하지 못하게 된다.
그렇게 되면, 이 모델은 실제 데이터의 성질을 잘 반영한 모델이 아니다!
3.4) 정리
이렇게!
3가지 가정에 따라 잔차가 평균으로 회귀하도록 만든 모델을 '회귀 모델'이라 할 수 있다.
'잔차의 특성'
- 위의 잔차에 대한 조건은 변수간의 선형 결합 관계에 대한 조건과 함께 거론됨
- 잔차의 성질은 선형회귀모델이 아니라도, 데이터 모델을 만들 때 염두해 둬야할 매우 중요한 정보!
- 데이터 모델의 성능을 측정할 때 R^2, RMSE, AUC 등의 값만 측정하지 말고, 잔차가 어떤 특성을 갖고 있는지를 분석하는 것이 필요!
2. Simple Linear Regression (단순 선형 회귀)
1) 기본개념

- 단순 선형 회귀모델의 기본식
- 단순 선형 회귀는 predictor(Xi)가 단 하나일 때의 케이스
ex) Yi: 샘플 내의 i번째 딸의 키, Xi: i번째 엄마의 키, ei: 에러
(ei는 평균0, 표준편차 σ^2 를 따른다.)
식을 완성할 β0, β1은 어떻게 구할까?
2) 회귀 계수 (regression coefficient)
β0, β1을 실제로 구할 수 없기에, (β0, β1은 모수이기 때문)
^β0, ^β1 (추정치)를 구해보자.
SSE를 이용해서 추정치를 구할 수 있다!!
* SSE (Sum of Squared Error) : 관측값(Y)과 추정값(^Y)의 차이들의 제곱합
이외에도 오차 정도를 측정하는 대표적인 방식들로,
| SAD (β0, β1) = Σ | Yi - (β0 + β1Xi) | | - 일반적으로 goodness of fit(적합도)을 측정하는데 쓰임 - 상대적으로 이상치 영향이 적은 편 - 절댓값이므로, 미분방식에 적용하겡 부적합 |
| L (β0, β1) = Σ L {Yi - (β0 + β1Xi) } | - 손실함수를 이용한 방식 - 경제학 에서 많이 사용 |
| SSE (β0, β1) = Σ { Yi - (β0 + β1Xi) }^2 | - Coefficient를 구하기 위한 LSE에 사용할 방식 - 크게 튀는 outlier에 영향을 많이 받음 (제곱이니까!) - 계산이 쉬운 편 |

2.1) 회귀계수 - LSE
Least Squared Error
최소 제곱법을 이용한 회귀계수 구하기
1) Unbiasedness(불편향성)
가정이 잘 충족됐다면 LSE는 불편향성을 가지게 된다!
이는 추정값의 기댓값(평균)이 모수에 근접하는 것을 의미한다.
2) Efficiency (효율성)
모든 불편추정량 중 최소의 분산을 가진다!
오차항의 분산값(σ^2)이 커질수록, LSE의 분산은 커지므로, 부정확한 결과를 초래한다.
X의 값이 넓게 퍼져있을 수록 LSE의 분산은 작아지고, X에 의한 Y의 변화에 대한 설명력이 높아진다.
3) Linearity (선형성)
Gauss-Markov Theorem (가우스 마코프 정리)
선형관계의 척도 중 무엇이 가장 적절한가를 결정해야 하는데,
조건 4개 or 5개를 충족하면 LSE가 가장 좋은 척도다! 라고 생각하는 이론.
* 조건 : 1) 오차항의 평균은 0 2) 오차항과 독립변수는 독립 3) 오차항의 독립성 4) 오차항의 등분산성 5) 오차항의 정규성
추가 예정
3. 가설 검증
4. 다중회귀 VS. 다항회귀
5. 다중공선성
'지식 > Machine Learning' 카테고리의 다른 글
| 데이터 전처리 (2. 피처 스케일링) (0) | 2021.04.11 |
|---|---|
| 데이터 전처리 (1) (0) | 2021.04.09 |
| 교차 검증 (0) | 2021.04.08 |
| ndarray, 리스트, 딕셔너리와 DataFrame 상호 변환하기 (0) | 2021.03.28 |
| K-NN 알고리즘의 쉬운 예제 (0) | 2021.03.16 |