머신러닝에는 지도학습(Supervised Learning)과 비지도 학습(Unsupervised Learning)이 있습니다.
지도학습에는
- 최근접 이웃 (Nearest Neighbor)
- 나이브 베이즈 (Naive Bayes)
- 의사결정 트리 (Decision Trees)
- 분류 규칙 학습자 (Classification Rule Learners)
- 선형 회귀 (Linear Regression)
- 회귀 트리 (Regression Trees)
- 모델 트리 (Model Trees)
- 신경망 (Neural Networks)
- 서포트 벡터 머신 (Support Vector Machines)
이 정도가 대표적인 알고리즘입니다. 그중 KNN은 가장 고전적/직관적인 방법이라고 알려져있습니다.
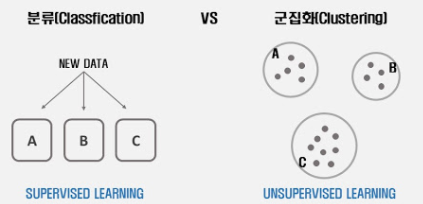
또한 K-NN은 '분류'에 속하는데, 분류를 군집화와 비교하여 설명하자면
분류 (Classification) - 라벨이 있는 지도 학습
군집화 (Clustering) - 라벨이 없는 비지도 학습
즉, 분류는 정답이 있는 데이터를 학습한 후, 새로운 데이터에 대해 예측하는 것이고
군집화는 정답이 없는 데이터에서 패턴을 찾아서 군집끼리 나누는 것입니다.
이해가 됐다면 다시 K-NN으로 돌아오겠습니다. K-NN은 '분류' 알고리즘 기법으로, 기본적인 로직은 단순합니다.
- 새로운 데이터와 가까운 거리에 위치한 몇 가지 라벨(데이터)을 함께 확인합니다.
- K개의 라벨들을 고려했을 때, 가장 빈도가 높은 것으로 새 데이터가 분류됩니다.
여기서 고려할 점은
1. K값을 몇으로 설정하는게 좋을까 입니다.
k값이 커지면 분류에서 이상치의 영향이 줄어들지만, 분류자체를 못하게 되는 상황이 발생합니다.
일반적으로는 총 데이터의 제곱근 값을 사용하고 있다고 합니다.
2. 가까운 거리 척도의 단위 - 표준화 (유클리드 거리)
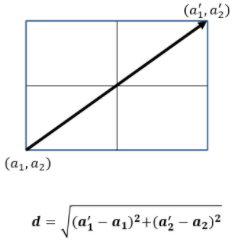
K=3으로 설정한다면, 유클리드 거리값을 기준으로 새 데이터와 가장 가까운 3개의 라벨들만 고려하여 그중 가장 빈도 높은 라벨로 분류가 되는 것입니다.
즉, 빈도가 높은 것의 기준은 K의 개수가 되는 것입니다.
장점
보면 느끼다싶이 1. 단순합니다.
2. 성능이 좋습니다.
3. 모델 훈련 시간이 필요없습니다.
사용방법
1. 거리 계산하기
2. 가장 근처에 있는 요소 뽑기 (k 기준)
3. 예측하기
0. 데이터 셋
# [x, y, type]
dataset = [[2.7810836,2.550537003,0],
[1.465489372,2.362125076,0],
[3.396561688,4.400293529,0],
[1.38807019,1.850220317,0],
[3.06407232,3.005305973,0],
[7.627531214,2.759262235,1],
[5.332441248,2.088626775,1],
[6.922596716,1.77106367,1],
[8.675418651,-0.242068655,1],
[7.673756466,3.508563011,1]]
1. 거리 계산하기
# 거리 계산하기 (유클리드 거리 공식): 루트((x2-x1)^2 + (y2-y1)^2))
from math import sqrt
# row = [x,y,type]
def euclidean_distance(row1, row2): # row1은 기존 label, row2는 새 data
distance = 0.0 # 초기화
for i in range(len(row1)-1): # 기존 label은 한 []에 3개(x,y,type)이므로, type을 뺀 2개로만 거리 계산.
distance += (row1[i]-row2[i])**2 # row1[i]:기존 label의 [x,y값], row2[i]:새 data의 [x,y]값
return sqrt(distance)
test =[3,3]
for row in dataset: # dataset에 있는 점들만큼 반복
distance = euclidean_distance(test, row)
print(distance) # 10개의 점들과 거리 차이
# 아래와 같이 거리차이 값 출력
0.2189163999999999
1.534510628
0.3965616879999998
1.61192981
0.06407232000000018
4.627531214
2.3324412480000003
3.922596716
5.675418650999999
4.673756466
2. 가장 근처에 있는 요소 뽑기 (k 기준)
def get_neighbors(train, test_row, num_neighbors): # 기존데이터,새데이터,k값
distances=list()
for train_row in train:
dist = euclidean_distance(test_row, train_row) # 기존데이터와 새 데이터의 거리 차이값(10개)
distances.append((train_row, dist)) # list에 기존데이터값, 거리차이값 저장
distances.sort(key=lambda tup: tup[1]) #dist를 기준으로 정렬.
neighbors = list()
for i in range(num_neighbors):
neighbors.append(distances[i][0]) # k값만큼 distance의 상위의 기존 라벨값 저장
return neighbors # k개의 기준 라벨(좌표) 반환좌표가 3,3이고, k=3으로 설정하여 구해보면
neighbors = get_neighbors(dataset, test, 3) # k=3
for neighbor in neighbors:
print(neighbor)
# 아래와 같이 가장 가까운 요소와의 거리차 출력
[3.06407232, 3.005305973, 0]
[2.7810836, 2.550537003, 0]
[3.396561688, 4.400293529, 0]3. 예측하기 - (1) 위처럼 판단할 예측 함수 생성
def predict_classification(train, test_row, num_neighbors):
neighbors = get_neighbors(train, test_row, num_neighbors) # k개의 좌표들
for neighbor in neighbors:
print(neighbor)
output_values = [row[-1] for row in neighbors] # 실제 type
prediction = max(set(output_values), key=output_values.count) # 마지막에 예측된 type출력
return prediction
(2) 테스트 데이터 입력하여 예측 값 확인하기
test = [6,5,0]
prediction = predict_classification(dataset, test, 3)
print('Expected %d, Got %d' % (test[-1],prediction))
# 아래와같이 출력
[7.673756466, 3.508563011, 1]
[3.396561688, 4.400293529, 0]
[7.627531214, 2.759262235, 1]
Expected 0, Got 1 # 가까운 type은 1이 많으므로 1로 예측
추가로 예측에 대한 정확도를 평가할 수 있는데,
평가 후에 정확도를 높이는 방법에는 Z-점수 표준화 방법, 데이터 셔플 등이 있습니다.
끝
[참고 혹은 사진 출처]
'지식 > Machine Learning' 카테고리의 다른 글
| 단순회귀, 다중회귀, 다항회귀 (0) | 2021.05.23 |
|---|---|
| 데이터 전처리 (2. 피처 스케일링) (0) | 2021.04.11 |
| 데이터 전처리 (1) (0) | 2021.04.09 |
| 교차 검증 (0) | 2021.04.08 |
| ndarray, 리스트, 딕셔너리와 DataFrame 상호 변환하기 (0) | 2021.03.28 |
