DFS와 BFS 문제를 풀기위해서는 무조건 알고 있어야하는 개념이 그래프입니다.
그리고 그래프를 구현하는 방법으로 인접행렬과 인접리스트가 있습니다.
이번 글에서는 각각의 장단점과 Java로 구현하는 것으로 마무리하겠습니다. (+LinkedList와 ArrayList의 장단점)
그래프
그래프란 요소들이 서로 복잡하게 연결되어 있는 관계를 표현하는 자료구조입니다.
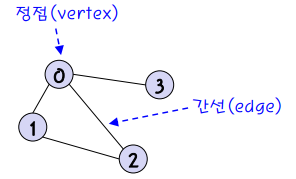
그래프에서 쓰이는 용어는
- 정점 (vertex) : 노드라고도 하며 데이터가 저장되는 원소
- 간선 (edge) : 링크라고도 하며 정점 간의 관계
- 그외에도 인접 정점, 차수, 경로 등의 용어가 있습니다.
그래프 구현
그래프를 구현하는 방법은 배열(Array)을 사용하는 인접 행렬, 리스트를 사용하는 인접 리스트가 있습니다.
그리고 인접 리스트를 구현하는 자료구조로 ArrayList와 LinkedList가 있습니다.
인접 행렬
그래프의 정점을 2차원 배열로 만들어서, 배열의 행과 열은 정점을 의미하며 각각의 원소들은 정점 간의 간선을 나타냅니다.
장점
- 2차원 배열에 모든 정점들의 간선 정보가 있기 때문에 두 정점을 연결하는 간선을 조회 시 O(1)의 시간복잡도로 가능합니다.
- 구현이 비교적 간단합니다.
단점
- 간선 수와 무관하게 항상 E² 크기의 2차원 배열이 필요하여 메모리 공간이 낭비됩니다.
- 그래프의 모든 간선(Edge)의 수를 알아내려면 인접 행렬 전체를 확인해야하므로 O(E²) 의 시간이 소요됩니다.
➕ 배열은 원소를 탐색하는데에는 O(1)의 시간이 소요되지만, 배열의 원소를 삭제하는 데에는 최악의 경우, O(N) 시간이 소요됩니다.
인접행렬 구현 (Java)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class 인접행렬로그래프 {
public static void main(String[] args) throws Exception {
BufferedReader br = new BuffredReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int pointN = Integer.parseInt(st.nextToken()); // 정점 수
int lineN = Integer.parseInt(st.nextToken()); // 간선 수
// 인접 행렬
boolean[][] adj = new boolean[pointN][pointN];
for (int i=0; i<lineN; i++) {
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
adj[from][to] = true;
adj[to][from] = true;
}
}
}
인접 리스트
정점(혹은 노드)와 정점 간의 연결을 리스트 형태로 나타냅니다.
배열을 생성하고 각각의 위치(Index)에 리스트를 생성하여 정점 간의 연결성을 구현하는 방법
장점
- 실제 연결된 노드들만 공간을 차지하기 때문에 모든 정점들의 원소의 합이 간선의 개수와 같습니다.
- 간선(Edge)의 개수에 비례하는 메모리 공간만 차지합니다. O(E)
단점
- 특정 노드(Vertex)가 연결된 노드가 무엇인지 확인하기 위해 모든 노드들을 확인해야하므로 O(V)만큼의 시간복잡도를 지닙니다.
- 구현이 덜 간단합니다.
인접 리스트 구현 (Java)
인접리스트는 ArrayList와 LinkedList를 이용하여 구현할 수 있습니다.
ArrayList 자료구조를 사용한 코드입니다.
import java.util.Scanner;
import java.util.ArrayList;
class 인접리스트로그래프_AR {
public static void main(String[] args) throws Exception {
Scanner sc = new Scanner(System.in);
int pointN = sc.nextInt(); // 정점 수
int lineN = sc.nextInt(); // 간선수
ArrayList<ArrayList<Integer>> arrListAdj = new ArrayList<>(pointN);
// 노드 1부터 보통 시작하므로 더미데이터 한개 추가해놓기
arrListAdj.add(new ArrayList<Integer>()); // Integer는 생략해도 괜찮다
for(int i=1; i < NODE_NUM; i++){
arrListAdj.add(new ArrayList<>());
}
// 양방향! 이므로 각각 추가해준다.
for (int i=0; i<lineN; i++) {
int n1 = sc.nextInt();
int n2 = sc.nextInt();
arrListAdj.get(n1).add(n2);
arrListAdj.get(n2).add(n1);
}
//출력
for (int i=1; i<= pointN; i++) {
Iterator<Integer> iter = arrListAdj.get(i).iterator();
System.out.println("[" + i + "]");
while (iter.hasNext()) {
System.out.print(iter.next() + " ");
}
System.out.println();
}
}
}
LinkedList 자료구조를 사용한 코드입니다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.StringTokenizer;
public class 인접리스트로그래프_LL {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int pointN = Integer.parseInt(st.nextToken()); // 정점 수
int lineN = Integer.parseInt(st.nextToken()); // 간선수
LinkedList<LinkedList<Integer>> adjLL = new LinkedList<>(); // idx 1부터 시작하는 인접리스트
// 미리 초기화
// 양방향! 이므로 각각 추가해준다.
for (int i=1; i<lineN; i++) {
st = new StringTokenizer(br.readLine(), " ");
int n1 = Integer.parseInt(st.nextToken());
int n2 = Integer.parseInt(st.nextToken());
adjLL.get(n1).add(n2); adjLL.get(n2).add(n1);
} // 출력
for (int i=1; i<adjLL.size(); i++) {
for (int j=1; j<adjLL.get(i).size(); j++) {
Iterator<Integer> iter = adjLL.get(i).iterator();
System.out.println("[" + i + "]");
while(iter.hasNext()) {
System.out.print(iter.next() + " ");
}
System.out.println();
}
}
}
}
ArrayList와 LinkedList의 차이
ArrayList
인덱스로 원소들을 관리할 수 있습니다.
배열과 상당히 유사하지만, 크기가 지정되면 변경불가한 배열과 달리, ArrayList는 클래스이기 때문에 원소 추가, 삭제가 가능합니다.
BUT 원소를 추가할 때 배열이 동적으로 늘어나는 것이 아닌, 더 큰 용량의 배열을 만들어 복사(Arrays.copyOf()) 작업을 진행합니다.
=> 비효율적입니다. ArrayList를 선언할 때는 초기용량을 설정하는 것이 좋을 듯 합니다 (예상이 어렵긴 합니다..)
정리
- 인덱스를 이용해 조회, 수정이 빠르다는 장점 (O(1)의 시간 복잡도)
- 중간 자리에 데이터 삽입&삭제가 빈번하게 발생한다면 비효율적이라는 단점
LinkedList

각 노드가 데이터와 포인터를 가지고 한 줄로 연결되어 있는 방식으로 데이터를 저장하는 자료 구조입니다.
내부적으로 양방향의 연결 리스트로 구성되어있어서 참조하려는 원소에 따라 순방향/역방향으로 순회할 수 있습니다.
배열의 단점을 보완하기위해 고안된 자료구조라는 점에서부터 ArrayList와 차이가 날 것 같습니다.
크기를 변경할 수 없고 비순차적인 데이터의 삽입&삭제에 비효율적이라는 배열의 단점을 보완하는 LinkedList는
중간에 원소를 삽입, 삭제를 할 때 각 데이터가 가리키는 주소값을 null 처리를 해주면 되기 때문에 빠릅니다.
하지만 배열의 장점을 갖고있지 못합니다.
인덱스를 통해서 검색하는 것이 아닌, Head에서부터 특정 원소까지 검색해야하므로 일반적으로 탐색 속도가 떨어집니다.
정리
- 원소를 삽입&삭제하는 경우 빠르다는 장점
- 첫번째 데이터의 추가/삭제 : O(1)의 시간 안에 수행
- 중간에 있는 데이터들의 추가/삭제 : 해당 데이터를 검색하는데까지 시간이 걸리기 때문에 O(n)의 수행시간
- 데이터 수가 많을 수록 접근성(조회)이 떨어진다는 단점 👉 B+tree 가 해결
➕ B+tree 자료구조
연결 리스트라고 해서 반드시 순차 탐색만 해야 한다는 법은 없습니다. B+tree 자료구조는 연결 리스트에 힙을 더한 것 같은 모양새를 갖고 있는데, 이는 데이터의 추가/삭제/정렬/조회 모두에 유리합니다.
그 구현이 복잡하다는 단점이 있지만, 직접 구현할 필요는 전혀 없습니다. 데이터베이스와 파일시스템이 B-tree의 구현체입니다.
👉 참고
인접 행렬과 인접 리스트 차이
- 공간 복잡도
- 인접 리스트 : 각 정점의 List에 간선 수만큼 저장하여 메모리 효율적으로 사용 O(V+E)
- 인접 행렬 : 정점의 수만큼 2차원 배열을 만들어 (모든 관계를 저장하므로) 노드 개수 많을 수록 메모리 낭비 ☹️ O(V²)
- 시간 복잡도
1. 두 노드가 인접한지 확인하는데 걸리는 시간
- 인접 리스트 : 선형 탐색으로 리스트 내 데이터들을 모두 탐색해야해서 최악의 경우 O(V)
- 인접 행렬 : 고유 인덱스 값으로 접근하여 O(1)
2. 한 노드에 연결된 모든 노드들을 확인하는데 걸리는 시간
- 인접 리스트 : 특정 정점에 연결된 간선 개수만큼 탐색하므로 O(E)
- 인접 행렬 : 특정 정점의 0이 아닌 경우를 모두 찾아야하므로 O(V)
참고
https://hongjw1938.tistory.com/23
https://devlog-wjdrbs96.tistory.com/64
'Algorithm & Data Structure > 개념' 카테고리의 다른 글
| [Concept] 인접 행렬과 인접 리스트 (0) | 2022.01.13 |
|---|---|
| java.lang.StringBuilder (가변적인 문자열) (0) | 2021.11.05 |
| [Concept] 재귀 용법 (0) | 2021.08.17 |
| 삽입 정렬 (0) | 2021.08.15 |
| 선택 정렬 (0) | 2021.08.15 |
![[Concept] 인접행렬과 인접 리스트(LinkedList, ArrayList)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbHFe4n%2FbtrvMHIOndV%2FAAAAAAAAAAAAAAAAAAAAACo0rEwsVt52uuAdZ3Tnw_qeLJRcRyHgwb5Nq8R0QaiC%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DK7zTjOtQhFoPcv1fApORLcuNCnk%253D)

