알고리즘에는 다양한 방법이 있습니다. 하나의 문제를 푸는데도 다양한 풀이 방법이 있는데, 이중 무엇이 정답이라고는 할 수 없지만, 더 나은, 더 좋은 알고리즘을 고를 수 있습니다.
그 (정량적인) 기준이 되는 것이 속도와 메모리공간입니다.
문제를 푸는 데에 빠르게 풀 수 있고, 더 적은 메모리양을 쓰는 알고리즘이 좋은 알고리즘이라 할 수 있습니다.
대표적으로 알고리즘의 복잡도를 계산할 때 시간복잡도와 공간복잡도를 체크합니다.
- 시간 복잡도: 알고리즘 실행 속도
- 공간 복잡도: 알고리즘이 사용하는 메모리 사이즈 ex)변수 사용갯수, 메모리 etc..
시간 복잡도
시간 복잡도는 말그대로 알고리즘을 실행하는데 걸리는 속도를 의미합니다.
프로그래밍에서 이 속도, 즉 시간 복잡도에 가장 영향을 많이 미치는 요소는 반복문입니다.
(가장 시간이 많이 걸리는 것이 반복문이기 때문에, 반복문에 따라서 성능이 어떻게 되는지 아는 것이 중요합니다.)
알고리즘 성능 표기법
평균을 고려할 것 같지만(세타 표기법), 보통 알고리즘의 경우 가장 최악의 상황에서 어느정도의 성능을 보장하는지를 체크하고자 합니다.
그래서 빅-오 표기법을 잘 알고 있어야 합니다.
- Big O (빅-오) 표기법: O(N)
- 알고리즘 최악의 실행 시간을 표기합니다.
- 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미
- 가장 많이/일반적으로 사용합니다.
- Ω (오메가) 표기법: Ω(N)
- 오메가 표기법은 알고리즘 최상의 실행 시간을 표기
- Θ (세타) 표기법: Θ(N)
- 오메가 표기법은 알고리즘 평균 실행 시간을 표기
대문자 O 표기법
- O(입력)
- 입력 n 에 따라 결정되는 시간 복잡도 함수
- O(1), O(𝑙𝑜𝑔𝑛), O(n), O(n𝑙𝑜𝑔𝑛), O(𝑛^2), O(2^𝑛), O(n!)등으로 표기합니다
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있습니다
- O(1) < O(𝑙𝑜𝑔𝑛) < O(n) < O(n𝑙𝑜𝑔𝑛) < O(𝑛^2) < O(2^𝑛) < O(n!)
- 참고: log n 의 베이스는 2 - 𝑙𝑜𝑔2𝑛
- O(1) < O(𝑙𝑜𝑔𝑛) < O(n) < O(n𝑙𝑜𝑔𝑛) < O(𝑛^2) < O(2^𝑛) < O(n!)
- 단순하게 입력 n에 따라, 몇번 실행이 되는지를 계산하면 됩니다.
- 표현식에 가장 큰 영향을 미치는 n 의 단위로 표기합니다.
- n이 1이든 100이든, 1000이든, 10000이든 실행을..
- 무조건 1회(상수회) 실행한다: O(1)
if n > 10: print(n) - n에 따라, n번, n + 10 번, 또는 3n + 10 번등 실행한다: O(n)
variable = 1 # 1번 for num in range(3): # 3번 for index in range(n): # n번 print(index) # 해당 코드의 시간복잡도는 3n+1 -> O(n) - n에 따라, 𝑛^2번, 𝑛^2 + 1000 번, 100𝑛^2 - 100, 또는 300𝑛^2 + 1번 실행합니다: O(𝑛^2)
variable = 1 # 1번 for i in range(300): # 300번 for num in range(n): # n번 for index in range(n): # n번 print(index) # 해당 코드의 시간복잡도는 300*n*n* + 1 -> O(n^2)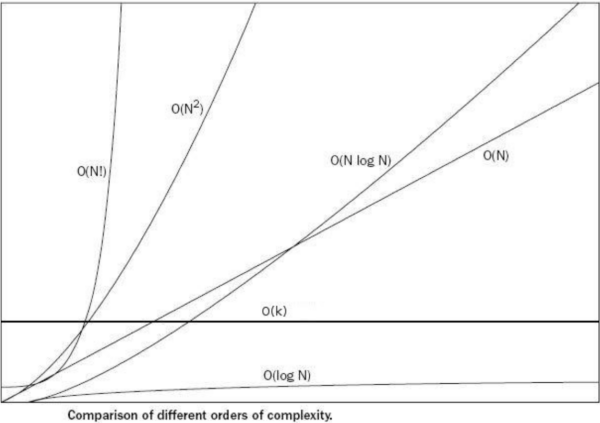
- 무조건 1회(상수회) 실행한다: O(1)
시간복잡도를 계산할 때, 상수 혹은 계수를 지우는 이유?
사실 n에 들어가는 입력값이 무한정으로 커질 때 상수, 혹은 계수는 그리 큰 영향을 미치지 못합니다.
가장 큰 차원 이외의 차원에도 마찬가지입니다.
3n^2 + 2n 이라 할지라도 입력값에 따라 가장 큰 영향을 미치는 것은 2n이 아닌 n^2입니다.
그렇기 때문에 3n^2 + 2n 의 값이 나와도 시간복잡도는 O(n^2)이 되는 것입니다.
1부터 n까지의 합을 구하는 알고리즘의 시간복잡도 구하기
1. 반복문 :입력 n에 따라 덧셈을 n 번 해야 한다.
def sum_all(n):
sum = 0
for i in range(1,n+1): # n의 계수에 따라 반복문은 n번 돕니다.
sum += i
return sum
sum_all(100) # 5050시간 복잡도: n, 빅-오 표기법은 O(n)
2. 수학적 지식 (n(n+1) / 2) 이용
def sum_all(n):
return (n * (n+1) /2)
sum_all(101)시간 복잡도: 1, 빅-오 표기법은 O(1)
무기한의 입력값을 가정했을 때는 2번의 방법이 더 좋은 성능의 알고리즘이라고 할 수 있습니다.
'Algorithm & Data Structure > 개념' 카테고리의 다른 글
| 버블 정렬 (0) | 2021.08.15 |
|---|---|
| [Concept] 해쉬 테이블 (Hash Table) (0) | 2021.08.10 |
| [Concept] 더블 링크드 리스트 (double linked list) (0) | 2021.08.04 |
| [Concept] 재귀함수와 연결리스트(linked list) (0) | 2021.08.02 |
| [Concept] 생성자와 소멸자 (0) | 2021.08.01 |
![[Concept] 시간 복잡도](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fbbboe3%2Fbtra8ALOwgB%2FAAAAAAAAAAAAAAAAAAAAAAkJ4Q2RhvZXjqL-5Sj34OkJiLTLdVH03dWceogLGsjL%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1761922799%26allow_ip%3D%26allow_referer%3D%26signature%3DnoxByNvU5v%252FL9U3ivxBjD2XxfBg%253D)